Whether you are working with addition and subtraction, multiplication and division, fractions or percentages, the concept of "part" forms a vital part of the math lesson.
Some examples:
In this chocolate bar, the whole is "5", so one piece is 1/5 of the whole. Fractions work when the size of the parts is the same for each piece.
We can also share a single piece with 4 friends and have one left over to keep. 5 ÷ 1 = 5
We can break off two pieces to make the subtraction sentence: 5 - 2 = 3
and then add them together again to make the whole bar: 3 + 2 = 5
In this lasagne, there are 5 columns, of which one is missing. Therefore, 5 - 1 = 4, or, there are 4/5 of a lasagne left. We can also say that 20% of the lasagne has been eaten.
In this carton of eggs, there are 12 eggs. Two of the eggs are white, one is blue, and the rest are brown. 2/12 or 1/6 of the eggs are white. 1/12 is blue. 9/12 or 3/4 are brown.
2 + 1 + 9 = 12
We can also say there are 6 pairs of eggs, or 6 x 2 eggs in the carton.
If we only want to use the brown eggs, we can remove the others: 12 - 3 = 9
We can divide the carton by rows, columns, pairs of columns, or into two equal columns 3 eggs wide. In doing so, we can investigate factors of 12, and experiment with various potential common denominators when exploring related fractions, and explore equivalent fractions.
Parts of the whole form a basis from which we can build on many mathematical concepts. We can extend this for use when speaking of angles, while referring to the circle (360 degrees) as the "whole" from which other angles are compared. This is, in fact, exactly how pie charts work.
We can even take this into polynomials by calculating the area of a deck for a pool:
If the pool is 8 m x 15 m, what is the area of a deck that surrounds it if the width of the deck has a universal width of 4 m?
The pool and the deck together become the "whole" combining the area of the pool and the area of the surrounding deck.
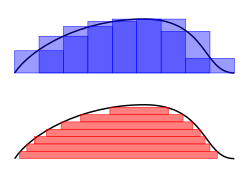
This concept, of parts making a whole, is also a vital part of integral calculus in which the area under an irregular curve is calculated.